Augmentation de données : cas pratique en Deep Learning avec TensorFlow

Introduction : Qu’est-ce que l’augmentation de données
L’augmentation de données est une technique utilisée en apprentissage automatique pour générer automatiquement des données d’entrainement supplémentaires par des transformations qui produisent des données similaires aux données réelles.
Cette technique est utile pour des scénarios où il est techniquement complexe, voire coûteux de collecter des données réelles, comme dans les domaines de la santé, de la sécurité ou de la recherche spatiale.
Aussi, dans les cas où les données d’entrainement sont limitées ou de mauvaise qualité, une telle mise en œuvre permet de créer de nouvelles données qui peuvent améliorer les performances du modèle d‘apprentissage automatique.
L’objectif de l’augmentation de données est de présenter au modèle d’autres aspects des données afin de permettre une meilleure généralisation.
Cas pratique
Voyons cela sur un exemple où le taux de bonnes réponses stagne trop rapidement :
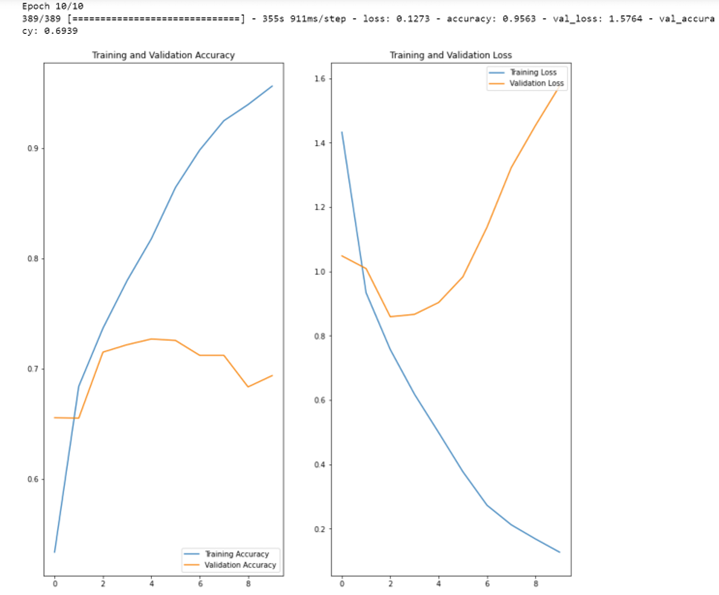
NB : x=nombre d’epochs, y=pourcentage de précision
Le graphe ci-dessus montre que la précision d’entraînement de notre modèle, en bleu, augmente de façon linéaire au fil des cycles d’apprentissage (epochs), tandis que la précision de validation, en orange, stagne.
De plus, l’écart de précision entre la précision d’entrainement et celle de la validation ne fait qu’augmenter dès le deuxième cycle : nous sommes ici confrontés au problème du surapprentissage.
Notons que moins nous avons de données d’apprentissage, et plus ce phénomène de surapprentissage intervient rapidement.
Nous allons donc tenter de résoudre cette problématique de surapprentissage par l’augmentation de données, en utilisant les couches de pré-traitement keras :
tf.keras.layers.RandomFlip ,
tf.keras.layers.RandomRotation
tf.keras.layers.RandomZoom
from tensorflow import keras
data_augmentation = keras.Sequential(
[
layers.RandomFlip("horizontal",
input_shape=(img_height,
img_width,
3)),
layers.RandomZoom(0.1),
]
)Nous avons ici créé une petite séquence de deux traitements simples de l’image :
• Un « flip » (inversion) horizontale ;
• Un zoom aléatoire jusqu’à 10%.
Le script ci-dessous nous affiche 9 versions de la première image de notre jeu d’images d’entraînement :
plt.figure(figsize=(10, 10))
for images, _ in train_ds.take(1):
for i in range(9):
augmented_images = data_augmentation(images)
ax = plt.subplot(3, 3, i + 1)
plt.imshow(augmented_images[0].numpy().astype("uint8"))
plt.axis("off")

Nous relançons l’apprentissage de notre réseau de neurones :
model = tf.keras.Sequential([
data_augmentation,
layers.experimental.preprocessing.Rescaling(1. / 255),
layers.Conv2D(64, (3, 3), padding='same', activation='relu'),
layers.MaxPooling2D((2, 2)),
layers.Conv2D(64, (3, 3), padding='same', activation='relu'),
layers.MaxPooling2D((2, 2)),
layers.Conv2D(128, (3, 3), padding='same', activation='relu'),
layers.MaxPooling2D((2, 2)),
layers.Conv2D(128, (3, 3), padding='same', activation='relu'),
layers.MaxPooling2D((2, 2)),
layers.Dropout(0.5),
layers.Flatten(),
layers.Dense(128, activation='relu'),
layers.Dense(num_classes)
])
Notons au passage que nous abandonnons l’apprentissage dès un écart de 50% entre les taux d’apprentissage et de validation, afin d’écourter l’apprentissage :
• c’est suffisant pour vérifier que le nombre de cycles d’apprentissage « utiles » aura augmenté ;
• cet abandon évite, quels que soient les taux de bonnes réponses, le phénomène de surapprentissage.
Compilons le modèle:
model.compile(optimizer='adam',
loss=tf.keras.losses.SparseCategoricalCrossentropy(from_logits=True),
metrics=['accuracy'])
model.summary()
Model: "sequential_2"
_________________________________________________________________
Layer (type) Output Shape Param #
=================================================================
sequential_1 (Sequential) (None, 180, 180, 3) 0
rescaling_2 (Rescaling) (None, 180, 180, 3) 0
conv2d_4 (Conv2D) (None, 180, 180, 64) 1792
max_pooling2d_4 (MaxPooling (None, 90, 90, 64) 0
2D)
conv2d_5 (Conv2D) (None, 90, 90, 64) 36928
max_pooling2d_5 (MaxPooling (None, 45, 45, 64) 0
2D)
conv2d_6 (Conv2D) (None, 45, 45, 128) 73856
max_pooling2d_6 (MaxPooling (None, 22, 22, 128) 0
2D)
conv2d_7 (Conv2D) (None, 22, 22, 128) 147584
max_pooling2d_7 (MaxPooling (None, 11, 11, 128) 0
2D)
dropout_1 (Dropout) (None, 11, 11, 128) 0
flatten_1 (Flatten) (None, 15488) 0
dense_2 (Dense) (None, 128) 1982592
dense_3 (Dense) (None, 13) 1677
=================================================================
Total params: 2,244,429
Trainable params: 2,244,429
Non-trainable params: 0
_________________________________________________________________
Entrainons le modèle, avec un maximum de 15 cycles d’apprentissage :
epochs =15
history = model.fit(
train_ds,
validation_data=val_ds,
epochs=epochs
)Le script ci-dessous nous permet d’afficher les courbes d’apprentissage et de validation :
acc = history.history['accuracy']
val_acc = history.history['val_accuracy']
loss = history.history['loss']
val_loss = history.history['val_loss']
epochs_range = range(epochs)
plt.figure(figsize=(8, 8))
plt.subplot(1, 2, 1)
plt.plot(epochs_range, acc, label='Training Accuracy')
plt.plot(epochs_range, val_acc, label='Validation Accuracy')
plt.legend(loc='lower right')
plt.title('Training and Validation Accuracy')
plt.subplot(1, 2, 2)
plt.plot(epochs_range, loss, label='Training Loss')
plt.plot(epochs_range, val_loss, label='Validation Loss')
plt.legend(loc='upper right')
plt.title('Training and Validation Loss')
plt.show()
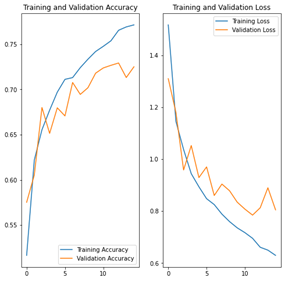
NB : x=nombre d’epochs, y=pourcentage de précision
Nous remarquons moins de surajustement qu’auparavant, et les taux de précision en entrainement et en validation restent très proches jusqu’à environ 10 cycles d’apprentissage. D’ailleurs, l’écart n’atteint visiblement pas 50% au bout du 15ème et dernier cycle.
Pour terminer, comparons les résultats des modèles sans et avec augmentation en catégorisant une image non comprise dans l’ensemble d’apprentissage ou de validation :
from pathlib import Path
imag_path="C:/Users/DataMindset/Downloads/deep_learning_images_2022_10_04/deep_learning_images/TEST image 2 novembre/fenetre/8.jpg
img = tf.keras.utils.load_img(
imag_path, target_size=(img_height, img_width)
)
img_array = tf.keras.utils.img_to_array(img)
img_array = tf.expand_dims(img_array, 0) # Create a batch
predictions = model.predict(img_array)
score = tf.nn.softmax(predictions[0])
print(
"Cette image ressemble plus à la catégorie {} à {:.2f} pour cent."
.format(class_names[np.argmax(score)], 100 * np.max(score))
)
Avec le modèle “initial sans augmentation”, nous obtenons :
Sortie : 1/1 [=============================] – 0s 44ms/pas
Cette image ressemble plus à la catégorie fenêtre à 64,96 pour cent.
Avec le modèle “augmenté”, nous obtenons :
Sortie : 1/1 [=============================] – 0s 44ms/pas
Cette image ressemble plus à la catégorie fenêtre à 94,69 pour cent.
Conclusion
En conclusion l’augmentation de données nous donne des meilleurs résultats pour deux raisons :
• Nous pouvons augmenter le nombre de cycles d’apprentissage sans tomber dans le surapprentissage.
• Il en résulte une meilleure catégorisation des données de test.





